Another C# class ready of my DWA (Digital Waveform Archive) audio data compression algorithm. This time it is well-known and much respected transform in the world of digital data compression - DCT (Discrete Cosine Transform). It seems to me that there is no such C# class available on the Internet, or at least Google can't find it, so this is like my Christmas gift to all digital data processing enthusiasts.
So, what is it, and why this transform is so important? Well, if we take any audio data block, we can see that it has a sequence of audio data and this audio data changes over time - so this is so-called time domain representation of information. By using Discrete Cosine Transform, we can transform this data into frequency domain representation. By doing this, we can get information about which audio signal frequencies exist in our audio data block. Let's take a look at the formula of the transform:
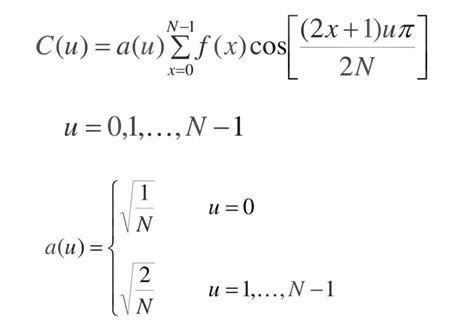
As any audio signal has a harmonic nature, we can represent it with a set of harmonic cosine functions. This way, we just calculate how much cosine functions with different frequencies exist in our audio signal. Basically, it works like any graphical audio equalizer - when you play a song, you can see nice graphical information about it, and Discrete Cosine Transform works the same way, but it has much more precision, and we can get our original audio signal back anytime by doing Inverse Discrete Cosine Transform.
Today, almost all popular audio compression algorithms such as MP3 use Modified Discrete Cosine Transform (MDCT) - as the name implies, basically it is the same Discrete Cosine Transform but slightly modified. Personally, I don't like it so much because it destroys the original waveform and introduces audible distortions - pre-echoes for example. If I have enough time, I'll make a MDCT (Modified Discrete Cosine Transform) C# class as well, so stay tuned.
Please note that to do a Discrete Cosine Transform we need to calculate too many cosine functions and such calculations take a lot of time even on powerful computers. My C# class has a fast implementation of the transform, here is my source code:


